

For this scenario, the mean weight wouldn’t change no matter how far along the line you move. Let’s suppose that the regression line was flat, which corresponds to a coefficient of zero. Consequently, we can’t shift along the line by a full meter for these data. In this case, the height and weight data were collected from middle-school girls and range from 1.3 m to 1.7 m.
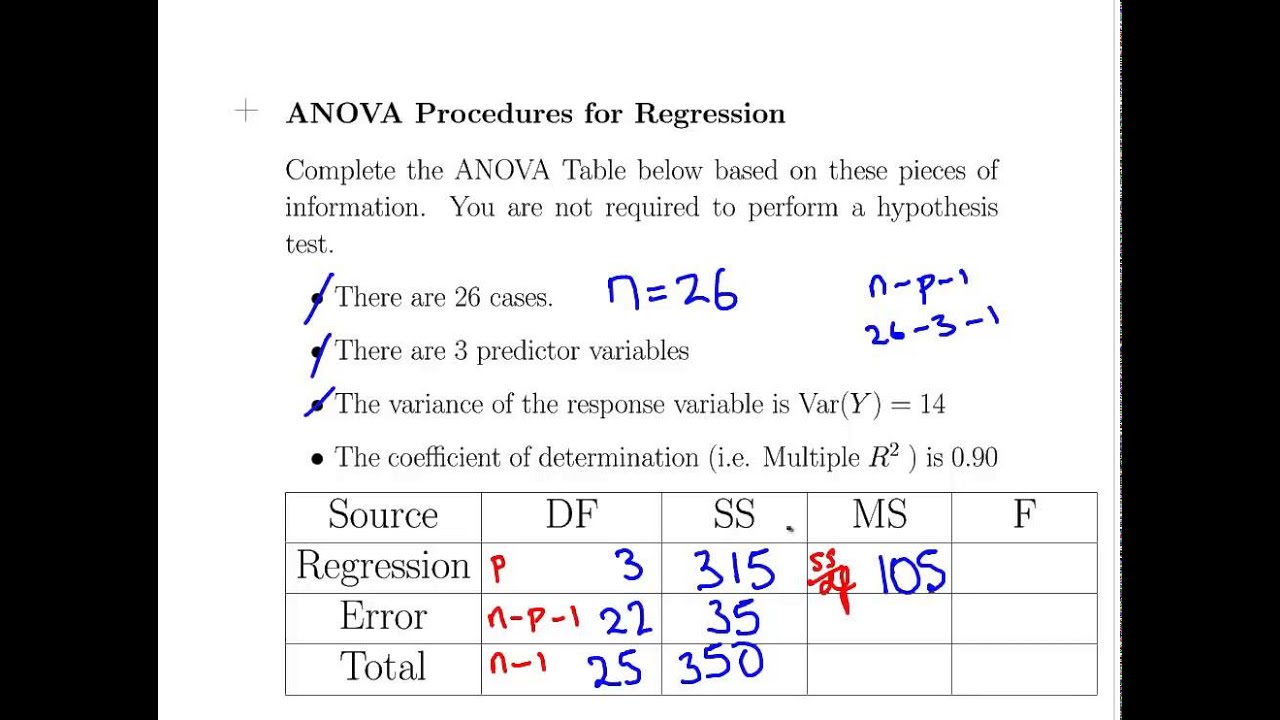
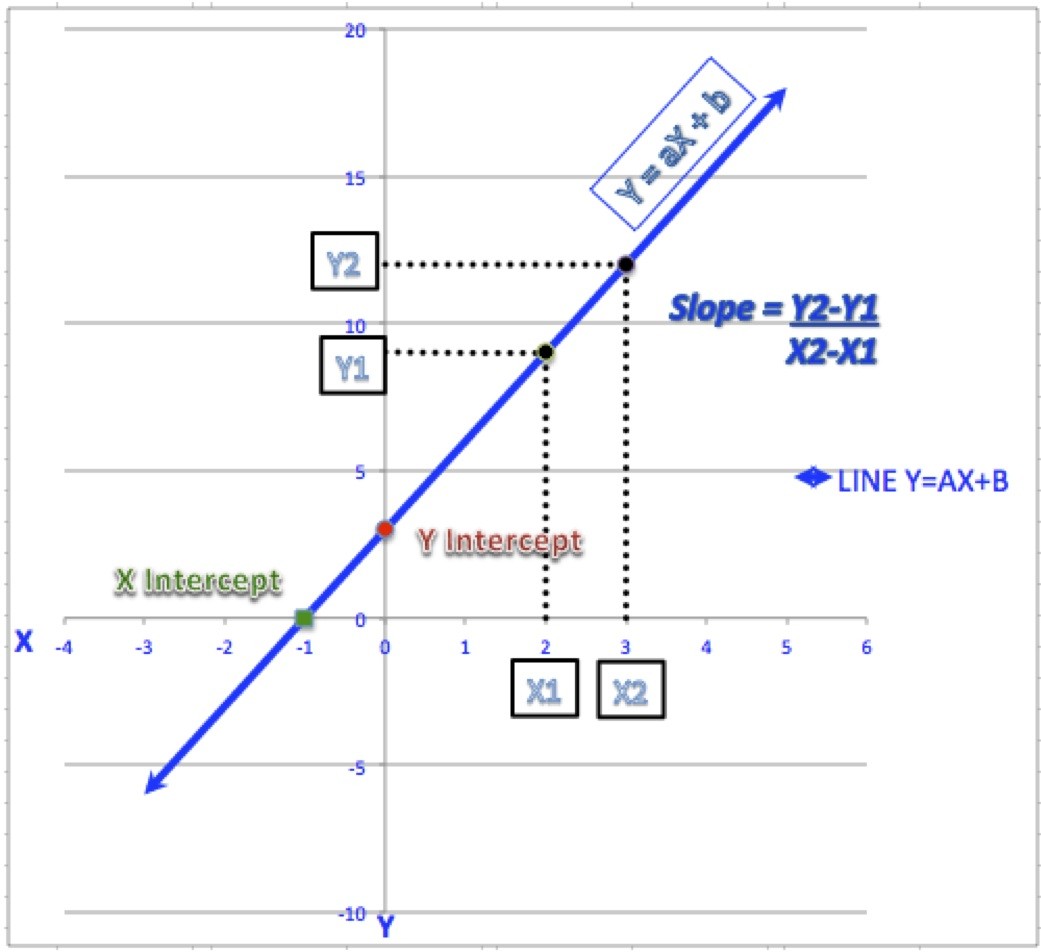
Keep in mind that it is only safe to interpret regression results within the observation space of your data. If you move to the right along the x-axis by one meter, the line increases by 106.5 kilograms. The regression line on the graph visually displays the same information. If your height increases by 1 meter, the average weight increases by 106.5 kilograms.
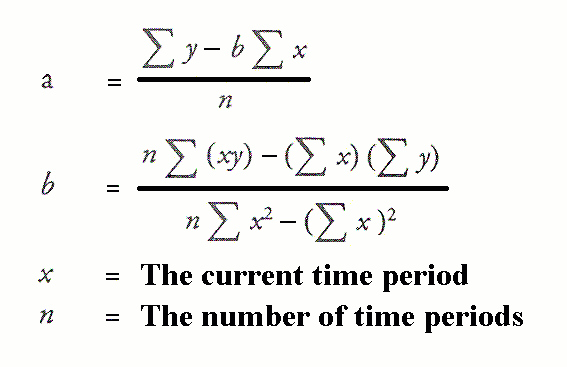
This coefficient represents the mean increase of weight in kilograms for every additional one meter in height. For example, if you wanted to generate a line of best fit for the association between height and shoe size, allowing you to predict shoe size on the basis of a person's height, then height would be your independent variable and shoe size your dependent variable).The height coefficient in the regression equation is 106.5. To begin, you need to add paired data into the two text boxes immediately below (either one value per line or as a comma delimited list), with your independent variable in the X Values box and your dependent variable in the Y Values box. This calculator will determine the values of b and a for a set of data comprising two variables, and estimate the value of Y for any specified value of X. The line of best fit is described by the equation ŷ = bX + a, where b is the slope of the line and a is the intercept (i.e., the value of Y when X = 0). This simple linear regression calculator uses the least squares method to find the line of best fit for a set of paired data, allowing you to estimate the value of a dependent variable ( Y) from a given independent variable ( X).


 0 kommentar(er)
0 kommentar(er)
